Вектор
Показаны 20 из 103 задач
Решение
Решение

Решение
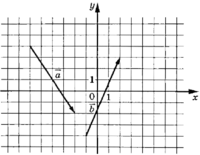
Решение
 и . Найдите скалярное произведение
и . Найдите скалярное произведение
Решение
Решение
Решение
Решение
Решение

Решение

Решение
Решение
Решение
Решение
Решение
Решение
Решение
Решение
Решение
Решение
