Решение иррациональных уравнений и неравенств
1. Иррациональная функция
Пусть дана иррациональная функция `y=sqrt f(x)`, имеющая переменную x под знаком корня. Если показатель корня чётный (2k), то такая функция определена (`D_y`) только для неотрицательных чисел и множество её значений (`E_y`) - множество неотрицательных чисел, т.е.:`underbrace(f(x)>=0)_{D_y} ; underbrace(sqrt(f(x)) >= 0)_{E_y}`
Следует помнить, что корень чётной степени из функции то же степени есть модуль этой функции:
`root(2K)(f^(2K)(x))=abs(f(x))`
Например: `sqrt(x^2)=abs(x); sqrt(x^2-2x+1)=abs(x-1)`
2. Решение иррациональных неравенств
2.1 Решение иррациональных неравенств со знаком меньше (меньше либо равно)
| `sqrt(f(x)) < phi(x) ` | `sqrt(f(x)) <= phi(x) ` |
| При `phi(x) < 0 ` неравенства не имеют решения (на уровне "здравого смысла") | |
| `{ (f(x) >=0), (phi(x)>0), (f(x) < phi^2(x)) :} ` | `{ (f(x) >=0), (phi(x)>=0), (f(x) <= phi^2(x)) :} ` |
Примеры решений иррациональных неравенств со знаком меньше (меньше либо равно)
2.1.1 Решить неравенство `sqrt(x+2) <= -x`
`{ (x+2 >= 0), (-x >= 0), (x+2 <= x^2) :} <=> { (-2 <= x <= 0), ( x^2 - x-2 >= 0) :} `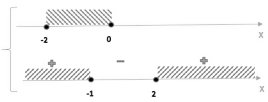
Ответ: [ -2; -1]
2.1.2 Решить неравенство `(x-1)sqrt(4-x^2) <= 0`
ОДЗ: `(2-x)(2+x) >=0`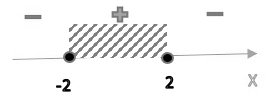
На ОДЗ `sqrt(4-x^2) >=0`
`x=2; x=-2`
В ОТВЕТ
При `x != +-2`
`sqrt(4-x^2) > 0 => ` осталось решить на ОДЗ неравенство `x-1 <= 0`:
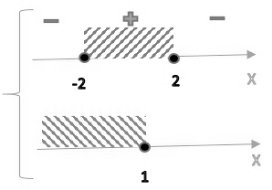
Ответ: `[-2; 1] uu {2}`
2.1.3 Решить неравенство `sqrt(6-x-x^2)/(x+4) <= sqrt(6-x-x^2)/(-2x+5)`
`{ (ОДЗ: x^2+x-6 <= 0), (x != -4), (x != 2.5) :}`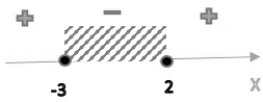
`x=-3; x=2`
В ОТВЕТ
При `x in (-3; 2) text { } sqrt(6-x-x^2) > 0`
Поделив на `sqrt(6-x-x^2)` обе части неравенства, получим: `1/(x+4)+1/(2x-5) <= 0`
`(2x-5+x+4)/((x+4)(2x-5)) <=0 ; (3x-1)/((x+4)(2x-5))<=0`
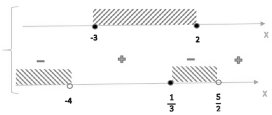
Ответ: `{-3} uu [1/3; 2]`
2.2 Решение иррациональных неравенств со знаком больше (больше либо равно)
Здесь работы "больше", по сравнению с решением неравенств со знаком меньше/меньше либо равно (см. п.2.1). Необходимо рассматривать два случая:1) `phi(x) > 0 (phi(x) >= 0)`, тогда неравенство выполняется для любых X из ОДЗ
2) `phi(x) < 0`
То есть необходимо решать совокупность двух систем и в ответ "идут" все значения, удовлетворяющие ИЛИ системе 1, ИЛИ системе 2:
| `sqrt(f(x)) > phi(x) ` | `sqrt(f(x)) >= phi(x) ` |
| `[(1 { (f(x) >=0), (phi(x)>0), (f(x) > phi^2(x)) :}), (2 {(f(x)>=0),(phi(x) < 0):}) :} ` | `[(1 { (f(x) >=0), (phi(x)>=0), (f(x) >= phi^2(x)) :}), (2 {(f(x)>=0),(phi(x) < 0):}) :} ` |
Примеры решений иррациональных неравенств со знаком больше (больше либо равно)
2.2.1 Решить неравенство `sqrt(x-3) > x-5`
`[({ (x >= 3), (x >= 5), (x-3 > x^2-10x+25) :}), ({(x >= 3),(x < 5):}) :}; [({ (x >= 5), ( x^2-11x+28 < 0) :}), (3 <= x < 5) :} `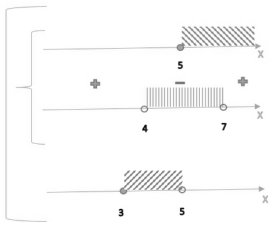
Ответ: [3; 7)
3. Решение иррациональных уравнений
3.1 Решить уравнение `8sqrt(12+16x-16x^2)+4x-4x^2=33`
`16sqrt(-4x^2+4x+3)+(-4x^2+4x+3)=36`ОДЗ: `4x^2-4x-3 <= 0`
`[(x=(2+sqrt(4+12))/4), (x=(2-sqrt(4+12))/4) :}`
ОДЗ:
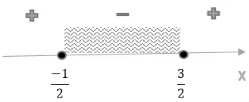
Обозначим `sqrt(-4x^2+4x+3)=t >= 0`
`{(t >= 0), (t^2+16t-36=0) :}; {(t >= 0), ([(t=2 vv ), (t=-18) :}) :}`
`t =2` Возврат к старой переменной:
`{(-1/2 <= x <=3/2), (sqrt(-4x^2+4x+3)=2 text{ (*)}) :} `
* `-4x^2+4x+3=4; 4x^2-4x+1=0; (2x-1)^2=0; x=1/2`
`{(-1/2 <= x <=3/2), (x=1/2) :} `
Ответ: `1/2`
3.2 Решить уравнение `sqrt(x^2+x+4)+sqrt(x^2+x+1)=sqrt(2x^2+2x+9)`
ОДЗ: `x in R``sqrt(x^2+x+1)=t > 0`
`x^2+x+1 = t^2; x^2+x+4=t^2+3`
`2x^2+2x+9 = 2t^2+7`
`sqrt(t^2+3)+t = sqrt(2t^2+7)`
Обе части больше 0 !
Возведём обе части в квадрат:
`2t^2+3+2tsqrt(t^2+3) = 2t^2 + 7;`
`2tsqrt(t^2+3) = 4;`
`tsqrt(t^2+3) = 2; t^2(t^2+3) = 4;`
`{(t^4+3t^2-4 = 0), (t > 0) :}; {(t > 0), ([(t^2 = 1), (t^2 = -4 text { нет действительных корней}) :}) :}`
`{(t > 0), ([(t=1 vv), (t=-1):}) :}`
Переход к старой переменной: `sqrt(x^2+x+1)=1; x(x+1)=0`
Ответ: -1; 0
3.3 Решить уравнение `(x^2+2x-4)*sqrt(x^2+7x+10) = 0`
` {(ОДЗ: x^2+7x+10 >=0 ), ([(x^2+2x-4 = 0), (sqrt(x^2+7x+10) = 0):}) :}`| ` {(), (), (), (), (), (),(), (), () :}` |
ОДЗ
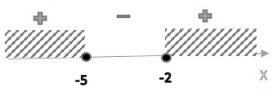
|
| ` [(x=-1-sqrt5), (x=-1+sqrt5), (x=-5), (x=-2) :}` |
Ответ: `-5; -2; sqrt5-1`
3.4 Решить уравнение `sqrt((2x+2)/(2+x))-sqrt((2+x)/(2x+2))=7/12`
Способ подстановки: `sqrt((2x+2)/(2+x))= t > 0``{(t > 0), (t-1/t-7/12=0) :}; {(t > 0), (12t^2-7t-12=0) :};`
`{(t > 0), ([(t=4/3 vv), (t=-18/24) :}) :}`
Переход к старой переменной:
`sqrt((2x+2)/(2+x))=4/3; (2x+2)/(2+x)=16/9`
`18x+18=32+16x; 2x=14; x=7`
Ответ: 7
3.5 Решить уравнение `sqrt(5+x-4sqrt(x+1))+sqrt(10+x-6sqrt(x+1))=1`
`sqrt((x+1)-4sqrt(x+1)+4)+sqrt((x+1)-6sqrt(x+1)+9)=1``sqrt((sqrt(x+1)-2)^2)+sqrt((sqrt(x+1)-3)^2)=1`
Корень чётной степени из функции той же степени есть модуль этой функции
`abs(sqrt(x+1)-2)+abs(sqrt(x+1)-3)=1`
`sqrt(x+1)-3=t`
`sqrt(x+1)-2=t+1`
`abs(t+1)+abs(t)=1`
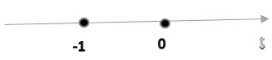
`[({(t <= -1), (-t-1-t=1; t=-1 vv):}), ({(-1 < t <= 0), (t+1-t=1; t in R):}), ({(t > 0), (2t+1=1; emptyset) :}):}`
`-1 <= t <= 0`
Переход к старой переменной:
`-1 <= sqrt(x+1) - 3 <= 0`
`{(ОДЗ: x+1 >= 0), (sqrt(x+1) <= 3), (sqrt(x+1) >= 2) :}; {(x >= -1), (x+1 <= 9), (x+1 >= 4) :};` `{(x >= -1), (x <= 8), (x >= 3) :}`
Ответ: [3; 8]
3.6 Решить уравнение `root(3)(x-2)+sqrt(x+1)=3`
Легко видеть, что `x=3` удовлетворяет данному уравнению. Левая часть исходного уравнения является возрастающей функцией, а правая - константой, следовательно x=3 - единственный корень.Ответ: x=3
База задач с решениями на неравенства с корнями: Решения иррациональных неравенств
База задач с решениями на уравнения с корнями: Решения иррациональных уравнений