Функция
Показаны 20 из 460 задач
Решение
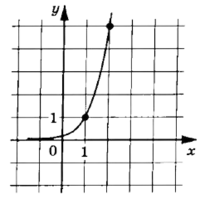 . Найдите f(4)
. Найдите f(4)
Решение

Решение

Решение
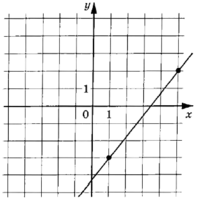
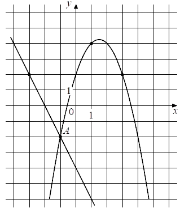 и , которые пересекаются в точках A и B. Найдите абсциссу точки B
и , которые пересекаются в точках A и B. Найдите абсциссу точки B
Решение
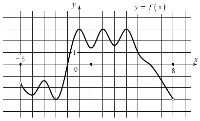
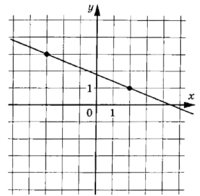
 изображен график функции Найдите значение x, при котором f(x)=0
изображен график функции Найдите значение x, при котором f(x)=0
Решение
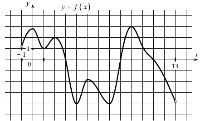
![На рисунке изображён график функции f(x), определённой на интервале (−5; 9). Найдите количество решений уравнения f'(x)=0 на отрезке [4; 9]](/content/images/solutions/4671.png) Найдите количество решений уравнения на отрезке [4; 9]
Найдите количество решений уравнения на отрезке [4; 9]
