Решение уравнений и неравенств, содержащих неизвестное под знаком модуля

1. Определение модуля

Модулем числа называется расстояние от точки, изображающей это число до нуля.
По определению `abs(f(x))>=0`, причём x - любое действительное число (`x in R`) из области допустимых значений (ОДЗ).

1.1 Модуль неотрицательного числа

Модуль неотрицательного числа есть само это число:
`abs(0)=0`;
`abs(5)=5`;
`abs(pi/3)=pi/3`;
`abs(sin 120°)=sin 120°=sqrt3/2`

1.2 Модуль отрицательного числа

Модуль отрицательного числа есть число, противоположное ему:
`abs(-7)=-(-7)=7`;
`abs(-e^4)=-(-e^4)=e^4`;

1.3 Модуль неизвестного числа

`abs(x)=[({(x >= 0),(abs(x) = x):}), ({(x < 0),(abs(x)=-x):}) :}`

1.4 Упражнения к определению модуля

1.4.1 Решить уравнение `abs(2x-1)=2x-1`

`2x-1>=0`; `x >= 1/2`
Ответ: `[1/2; +infty)`

1.4.5 Решить неравенство `abs(x+4) <=1`

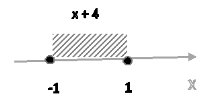
`-1 <= x+4 <= 1`;
`-5 <= x <= -3`
Ответ: `[-5; -3]`

1.4.6 Решить неравенство `1/5 abs(1-7x) > 3`

`abs(1-7x) > 15`;


`[(1-7x > 15), (1 - 7x < -15) :}`; `[(7x < -14), ( 7x > 16) :}`;
`[(x < -2), (x > 16/7) :}`
Ответ: `(-infty; -2) uu (16/7; +infty)`

2. Решение уравнений, содержащих неизвестную функцию под знаком модуля

- Если `varphi(x) < 0`, уравнение не имеет решения (по определению модуля).
- Если `varphi(x) >= 0`, то решаем систему:

`{( varphi(x) >= 0 ), ( [(f(x)=varphi(x)), (f(x)=-varphi(x)) :}) :}`

Примеры уравнений, содержащих неизвестную функцию под знаком модуля

Решить уравнение `abs(x^2-x)=3x-4`

`{( 3x-4 >= 0 ), ( [ (x^2-x=3x-4), (x^2-x=4-3x) :}) :}`; `{ (x >= 4/3 ), ( [ (x^2-4x+4 = 0), (x^2+2x-4=0) :}) :}`;

`[( { (x >= 4/3), ((x-2)^2=0) :} ), ( { (x >= 4/3), (x^2+2x-4=0) :}) :}`; `[( { (x >= 4/3), (x=2) :} ), ( { (x >= 4/3), ([(x=-1-sqrt5),(x=-1+sqrt5):}) :}) :}`;
Сравним `4/3 vv sqrt5-1` `4 vv 3sqrt5-3`; `7 vv 3sqrt5`; `49 vv 45 (>)`
`4/4 > sqrt5-1`
Ответ: 2

3. Решение неравенств, содержащих неизвестную функцию под знаком модуля

3.1 Смысл неравенства меньше либо равно

Если `varphi(x) < 0` - неравенство не имеет решений
Если `varphi(x) >= 0` - то необходимо решить систему: `{(varphi(x) >= 0), (-varphi(x) <= f(x) <= varphi(x)) :}`
`{(varphi(x) >= 0), (f(x) <= varphi(x)), (varphi(x) >= -f(x)) :}`

Примеры с модулем на неравенства со смыслом меньше либо равно

3.1.1 Решить неравенство `abs(1-3x^2) <= 4x`

`{(x >= 0), (1-3x^2 <= 4x), (1-3x^2 >= -4x) :}`; `{(x >= 0), (3x^2+4x -1 >= 0), (3x^2 - 4x -1 <= 0) :}`

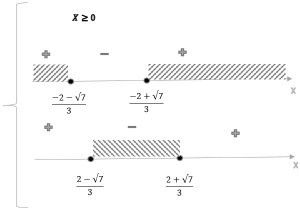
Ответ: `[(sqrt7-2)/3; (sqrt7+2)/3 ]`

3.1.2 Найти область определения функции `f(x)=sqrt(7-abs(x-2)/(3x+5))`

`D_f(x)`:
`7-abs(x-2)/(3x+5) >= 0`; `(21x+35-abs(x-2))/(3x+5) >= 0`; `[({(x >= 2), ((20x+37)/(3x+5) >= 0) :}), ({(x < 2), ((22x+33)/(3x+5) >=0 ) :}):}`

Сравним:`-37/20 vv -5/3`	Сравним: `-3/2 vv -5/3`
`37/20 ^^ 5/3`	`3/2 ^^ 5/3`
`111 ^^ 100`	`9 ^^ 10`
`111 > 100`	`9 < 10`
`-37/20 < -5/3`	`-3/2 > -5/3`

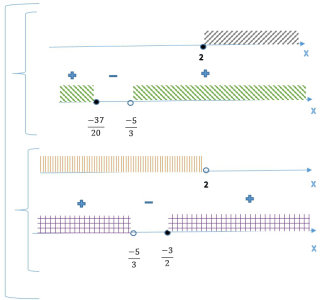
Итоговое объединение двух систем: `x < -5/3 uu [-3/2; 2] uu x>=2`


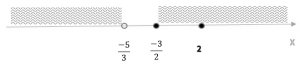
Ответ: `(-infty; -5/3) uu (-3/2; +infty)`

3.1.3 Найти область определения функции `f(x)=sqrt(1/2-abs(3/(5-x))`

`D_f(x)`:
`1/2-abs(3/(5-x)) >= 0`;
`abs(3/(5-x)) <= 1/2`;
` -1/2 <= 3/(5-x) <= 1/2`;

`{( 3/(5-x) <= 1/2), ( 3/(5-x) >= -1/2) :}`; `{( 3/(5-x) - 1/2 <= 0), ( 3/(5-x) + 1/2 >= 0):}`;

`{( (6-5+x)/(2(5-x)) <= 0 ), ( (6+5-x)/(2(5-x)) >= 0 ):}`; `2 > 0`; `{( (x +1)/(5-x) <= 0 ), ( (11-x)/(5-x) >= 0 ):}`;

Ответ: `(-infty; -1] uu [11; +infty)`

3.1.4 Найти область определения функции `f(x)=sqrt((x^2-7abs(x)+10)/(-x^2+6x-9))`

`D_f(x)`:
`[ ( { (x >= 0), ( ((x-2)(x-5))/(-(x-3)^2) >= 0) :} ), ( {(x < 0), ( ((x+2)(x+5))/(-(x-3)^2) >= 0) :} ) :}` ; `[ ( { (x >= 0), ( ((x-2)(x-5))/(x-3)^2 <= 0) :} ), ( {(x < 0), ( ((x+2)(x+5))/(x-3)^2 <= 0) :} ) :}`

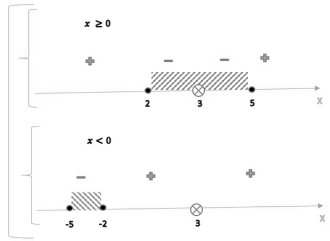
Ответ: `[-5; -2] uu [2; 3) uu (3; 5]`

3.2 Смысл неравенства больше либо равно

Если `varphi(x) <= 0` - то неравенство справедливо для всех `x`, удовлетворяющих области допустимых значений (ОДЗ).
Если `varphi(x) > 0` - то необходимо решить совокупность двух неравенств:

`[(f(x) >= varphi(x)), (f(x) <= -varphi(x)) :}`

Примеры с модулем на неравенства со смыслом больше либо равно

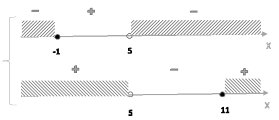
3.2.1 Решить неравенство `abs((x+1)/(x-1)) >= 1-2x`

а) `{(ОДЗ: x != 1), (1-2x < 0) :}`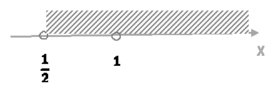

В ответ: `(1/2; 1) uu (1; +infty)` (a)

б) `{(ОДЗ: x != 1), (1-2x >= 0), ([((x+1)/(x-1) >= 1-2x), ((x+1)/(x-1) <= 2x - 1) :} ) :}`; `{(x <= 1/2), ([((x+1)/(x-1) + (2x -1)/1 >= 0), ((x+1)/(x-1)+ (1-2x)/1 <= 0) :} ) :}`;

`{(x <= 1/2), ( [ ((x^2-x+1)/(x-1) >= 0), ((1-x)^2/(x-1) <= 0) :} ) :}`; `[({(x <= 1/2), (x-1 > 0):}), ({(x <= 1/2), (-(x+1) <= 0):}) :}`; `[(emptyset), ({(x <= 1/2), (x+1 >= 0):}) :}`; `{(x <= 1/2), (x >= -1):}`
В ответ: `[-1; 1/2]` (б)
В ответ `[ ( a: (1/2; 1) uu (1; +infty)), ( б: [-1; 1/2]) :}`

Ответ: `[-1; 1) uu (1; +infty)`

4. Уравнения и неравенства, содержащие неизвестные под несколькими модулями

4.1 Решить неравенство `abs(x-4)-2abs(1-x) >= 1`

На числовом луче отметим значения x, при которых подмодульные значения обращаются в "0": `x=1; x=4`. Луч разбился на три интервала.


Необходимо на каждом интервале найти решение данного неравенства, то есть решить совокупность трёх систем неравенств:
`[ ( { (x <= 1), (4-x-2(1-x) >= 1) :} ), ( {(1 < x <= 4), (4-x+2(1-x) >= 1) :} ), ( {(x > 4), (x-4+2(1-x) >= 1) :} ) :}` ; `[ ( { (x <= 1), (4-x-2+2x >= 1) :} ), ( {(1 < x <= 4), (4-x+2-2x >= 1) :} ), ( {(x > 4), (x-4+2-2x >= 1) :} ) :}` ;

`[ ( { (x <= 1), (x+1 >= 0) :} ), ( {(1 < x <= 4), (5-3x >= 0) :} ), ( {(x > 4), (-x-3 >= 0) :} ) :}` ; `[ ( { (x <= 1), (x >= -1) :} ), ( {(1 < x <= 4), (x <= 5/3) :} ), ( {(x > 4), (x <= -3) :} ) :}` ;


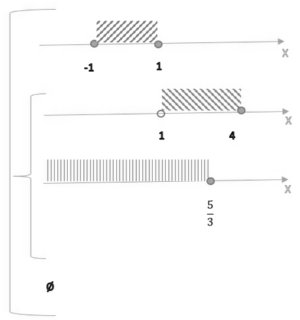
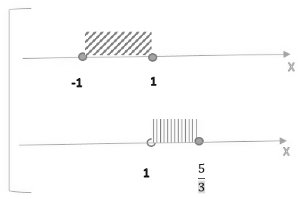
Ответ: `[-1; 5/3]`

4.2 Решить неравенство `abs(x) >= abs (7-x)`

Обе части данного неравенства неотрицательные. Возведя обе части в квадрат, мы получим неравенство того же смысла: `x^2 >= (7-x)^2` ` color{brown}{ text{Замечание: Если } a > 0 text{ и } b >0 text{ можно перейти от сравнения } a text{ и } b text{ к сравнению } a^2 text{ и } b^2 }`
`x^2 - (7-x)^2 >= 0; (x-7+x)(x+7-x) >= 0; 2x-7 >=0`
Ответ: `[7/2; +infty)`

4.3 Решить уравнение `abs(x^3-49x) + abs (49x^2-1) = x^3 +49x^2 -49x -1`

` color{brown}{ text{Замечание: Полезно помнить: }`
` color{brown} { text{Если } abs(a) +abs(b)=a+b text{ то } {(a>=0), (b >=0):} }`
`underbrace(abs(x^2-49x))_{\text{a}} + underbrace(abs (49x^2-1))_{\text{b}}`
Решение данного уравнения сводится к решению системы неравенств
`{(x^3 - 49x >= 0), (49x^2 -1 >= 0):}; {(x(x-7)(x+7) >= 0), ((7x-1)(7x+1) >= 0):}`


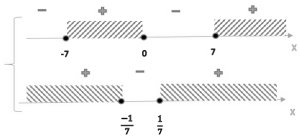
Ответ: `[-7; -1/7] uu [7; +infty)`

4.4 Решить уравнение `abs(x^2-9) + abs(x+3) = x^2 +x-6`

`underbrace(abs(x^2-9))_{\text{a}} + underbrace(abs(x+3))_{\text{b}}=underbrace(x^2 +x-6)_{\text{a+b}}`
`{(x^2-9 >= 0), (x+3 >= 0) :}`


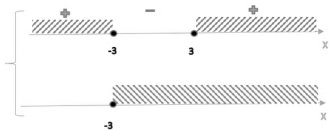
Ответ: `{-3} uu [3; +infty)`

4.5 Решить неравенство `3x-abs(x+10) - abs (2-x) <= 6`

`[ ( { (x <= -10), (3x+x+10-2+x <= -6) :} ), ( {(-10 < x <= 2), (3x-x-10-2+x <= -6) :} ), ( {(x > 2), (3x-x-10+2-x <= -6) :} ) :}` ; `[ ( { (x <= -10), (5x <= -14) :} ), ( {(-10 < x <= 2), (3x <= 6) :} ), ( {(x > 2), (x <= 2) :} emptyset ) :}` ;

`[(x <= -10), (-10 < x <= 2):}`


Ответ: `(-infty; 2]`

5. Неравенства, содержащие модуль, повышенной сложности

5.1 Решить неравенство `(abs(x-7)-abs(x+5)) / (abs(x-3) - abs(x+1)) < (abs(x-3) + abs(x+1)) / abs(x+5)`

Умножим обе части неравенства на функцию `g(x)=(abs(x-7)+abs(x+5)) / (abs(x-3) + abs(x+1)), g(x) > 0, text{ для } forall x in R`
`((x-7)^2-(x+5)^2) / ((x-3)^2 - (x+1)^2) < (abs(x-7) + abs(x+5)) / abs(x+5) <=>`

`((x-7-x-5)(x-7+x+5)) / ((x-3 -x -1)(x-3 +x +1)) < (abs(x-7) + abs(x+5)) / abs(x+5) <=>`

`(-12(2x-2)) / (-4(2x-2)) < (abs(x-7) + abs(x+5)) / abs(x+5) <=>`

`{(2x-2 != 0), (x+5 != 0), (3abs(x+5) < abs(x-7)+abs(x+5)) :} <=> {(x != 1), (x != -5), (2abs(x+5) < abs(x-7)) :}`

`{(x != 1), (x != -5), ((2x+10-x+7)(2x+10+x-7) < 0) :} <=> {(x != 1), (x != -5), ((x+17)(x+1) < 0) :}`

Ответ: `(-17; -5) uu (-5; -1)`

5.2 Решить неравенство `((x^2-5x+9)^2-4abs(x^2-5x+9)abs(x-6)+3(x-6)^2) / (2x^2+7x-15) <= 0`

`color{brown}{ text{Заметим: } x^2=abs(x)^2`
`(abs(x^2-5x+9)^2-4abs(x^2-5x+9)abs(x-6)+4abs(x-6)^2-abs(x-6)^2) / ((2x-3)(x+5)) <= 0 <=>`

`((abs(x^2-5x+9)-2abs(x-6))^2-abs(x-6)^2) / ((2x-3)(x+5)) <= 0 <=>`

`((abs(x^2-5x+9)-3abs(x-6))(abs(x^2-5x+9)-abs(x-6))) / ((2x-3)(x+5)) <= 0 <=>`

`((x^2-5x+9-3x+18)(x^2-5x+9+3x-18)(x^2-5x+9-x+6)(x^2-5x+9+x-6)) / ((2x-3)(x+5)) <= 0 <=>`

`((x^2-8x+27)(x^2-2x-9)(x^2-6x+15)(x^2-4x+3)) / ((2x-3)(x+5)) <= 0 <=>`

`x^2-8x+27 > 0 text{ для } forall x in R`
`x^2-6x+15 > 0 text{ для } forall x in R`
`x^2-2x-9=0; [(x=1-sqrt10), (x=1+sqrt10):}`
`x^2-4x+3=0; [(x=1), (x=3):}`


Ответ: `(-5; 1-sqrt10] uu [1; 3/2) uu [3; 1+sqrt10)]`

6. Примеры с модулями для самостоятельного решения с ответами

6.1 Решить неравенство `abs(x^2-16x+36) <= abs(36 -x^2)`

Ответ: `[0; 4.5] uu [8; +infty)`

6.2 Решить неравенство `abs(x^2-6x-2) >= abs(x^2 +7x+11)`

Ответ: `(-infty; -1]`

6.3 Решить неравенство `abs(4x^3-x+7) <= abs(2x^3 +5x+3)`

Ответ: `[-2; -1] uu {1}`

6.4 Решить неравенство `abs(x^3-x^2-5) <= abs(x^3 -5x^2+x-1)`

Ответ: `(-infty; -1] uu [1; 3]`

6.5 Решить неравенство `abs((x^2-2x+1)/(x-3)) >=1`

Ответ: `(-infty; -1] uu [2; 3) uu (3; +infty)`

6.6 Решить неравенство `(abs(2x-1)-abs(x+1))/(abs(2x+3) - abs(x-3)) <= 0`

Ответ: `(-6; 0) uu (0; 2]`

6.7 Решить неравенство `(abs(x^2-4x+3)-abs(x^2+x-3))/(abs(7x-3) - abs(3x-2)) <= 0`

Ответ: `[0; 1/4) uu (1/2; 1.2] uu [1.5; +infty)`

6.8 Решить неравенство `abs(x^2-5abs(x)+4) <= abs(2x^2 -3abs(x)+1)`

Ответ: `(-infty; -5/3] uu {-1} uu {1} uu [5/3; +infty)`

6.9 Решить неравенство `3x - abs(x+8) - abs(1-x) <= -6`

Ответ: `(-infty; 1]`
Много задач с решениями на неравенства с модулем можно посмотреть здесь:
Решения неравенств с модулем