Окружность с центром O проходит через вершины B и C большей боковой стороны прямоугольной трапеции ABCD и касается боковой стороны AD в точке T

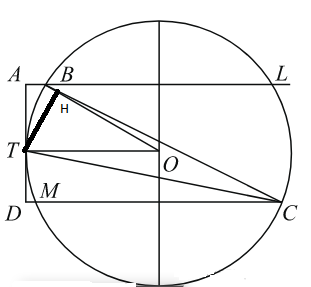
Окружность с центром `O` проходит через вершины `B` и `C` большей боковой стороны прямоугольной трапеции `ABCD` и касается боковой стороны `AD` в точке `T`. Точка `O` лежит внутри трапеции `ABCD`. а) Докажите, что угол `BOC` вдвое больше угла `BTC`. б) Найдите расстояние от точки `T` до прямой `BC`, если основания трапеции `AB` и `CD` равны `4` и `9` соответственно.
Решение 1004
а) Сделаем дополнительное построение: продолжим `AB` за точку `B` до её пересечения с окружностью `O` в точке `L`; соединим точку `O` с точкой `T`. Угол `BTC` измеряется половиной дуги `BLC` как вписанный в окружность `O`.
Угол `BOC` — центральный угол, измеряется целой дугой `BLC`. Следовательно, `/_BTC=(1/2)/_BOC`. Что и требовалось доказать.
б) Обозначим `OT=r`. `OT || AL || CD`. Диаметр окружности `O`, перпендикулярный `OT`, делит каждую из хорд `BL` и `CD` пополам.
`AL=2r-4`
`DM=2r-9`.
Применим теорему Пифагора для треугольника `TAB`: `TB^2=AT^2+AB^2` (1).
По теореме о касательной и секущей: `AT^2=AB*AL=4(2r-4)` (2)
Из (1) и (2) следует `TB^2=4(2r-4)+16=8r => TB=sqrt(8r)` Аналогично: `TC^2=18r => TC=sqrt(18r)`
Треугольник `TBC` вписан в окружность `O`. По теореме синусов `BC = 2r · sin /_BTC`.
Сделаем дополнительное построение: `TH _|_ BC` ; Обозначим `TH=h` - это искомое расстояние.
Площадь треугольника `BTC` : `S_(BTC)=(1/2)h*BC=(1/2)TB*TC*sin/_BTC`
Отсюда получаем, что `h*2r*sin/_BTC=sqrt(8r)*sqrt(18r)*sin/_BTC`
Следовательно: `h=sqrt(4*9)=6`
Ответ: `6` )