РЕШЕНИЕ
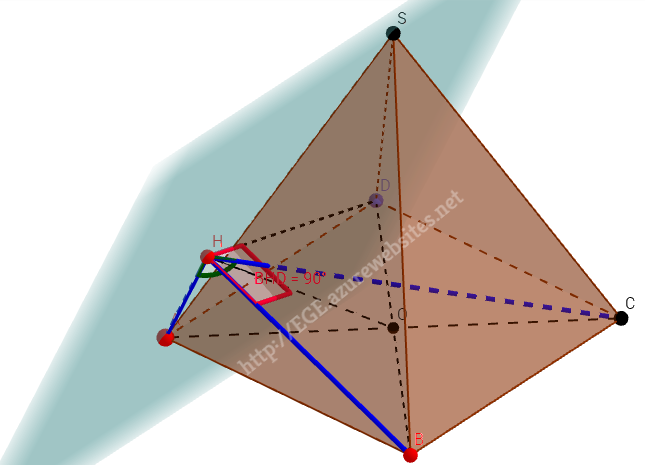
а) Рассмотрим треугольник `HBD`. Угол `BHD=90^@`, так как `BH` - `bot` на плоскость `ASD`, следовательно, `bot` к HD, лежащей в этой плоскости.
HO - медиана гипотенузы BD, значит равна её половине: `HO=(1/2)BD`; `AC=BD` по условию, следовательно `HO=(1/2)AC`, поэтому треугольник `AHC` - прямоугольный, что и требовалось доказать.
б)
`AC=sqrt((AH)^2+(HC)^2)=sqrt(26)` по теореме Пифагора. Следовательно,сторона основания пирамиды равна `sqrt13`.
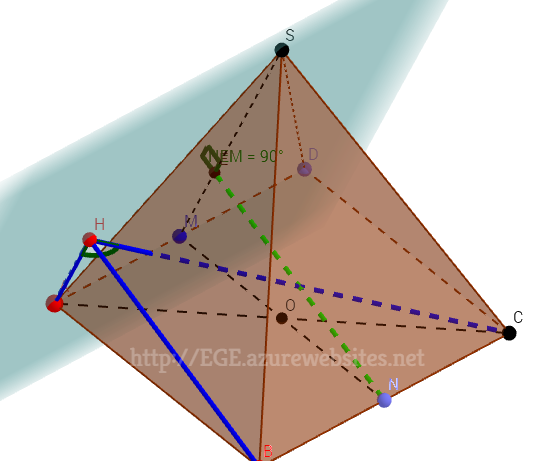
Дополнительное построение:
Через точку О проведём MN || CD; Проведём NE `_|_` к SM.
AD `_|_` к MN и AD `_|_` к SO, следовательно AD `_|_` к плоскости SMN по теореме о двух перпендикулярах.
Плоскость SAD проходит через AD, следовательно плоскости SAD и SMN взаимно `_|_`.
NE `_|_` к ME по построению, следовательно NE `_|_` к ASD.
Точки B и N лежат на прямой BC || плоскости ASD, следовательно NE=BH. AB=MN. Следовательно AH=ME=1 (если наклонные равны, то равны и их проекции на плоскость ASD).
Треугольник `MNE` подобен треугольнику `SMO`(они прямоугольные и имеют общий угол M); Отсюда следует, что `MS=(MO*MN)/(EM)=13/2`; `SO=sqrt(169/4-13/4)=sqrt(39)`.
Объём парамиды равен `(1/3)S_(ABCD)*SO`. Площадь основания равна 13. `SO=sqrt(39) => V_(SABCD) =(13sqrt(39))/3`
Ответ: `(13sqrt39)/3`
)

